Vibration Analysis for beginners 5
25.01.2024
1. What is important to know about signal processing?
2. What are the basic rules for evaluating machine vibration?
The signal from a vibration sensor is in analogue form. In order to work with it in analysers, the signal must be converted to digital form. This conversion is done by an A/D converter.
If the original continuous signal contains frequencies higher than half the sampling frequency, the signal will be distorted by the phenomenon known as aliasing.
Now we have a digital signal in the vibration analyser and we can work with it. For example, we can display it in its time-domain form - the time waveform. However, a more informative representation is the frequency domain. As shown in the previous video, the spectrum reveals the frequencies that compose the vibration signal. To calculate the spectrum, we use the Fast Fourier Transform (FFT).
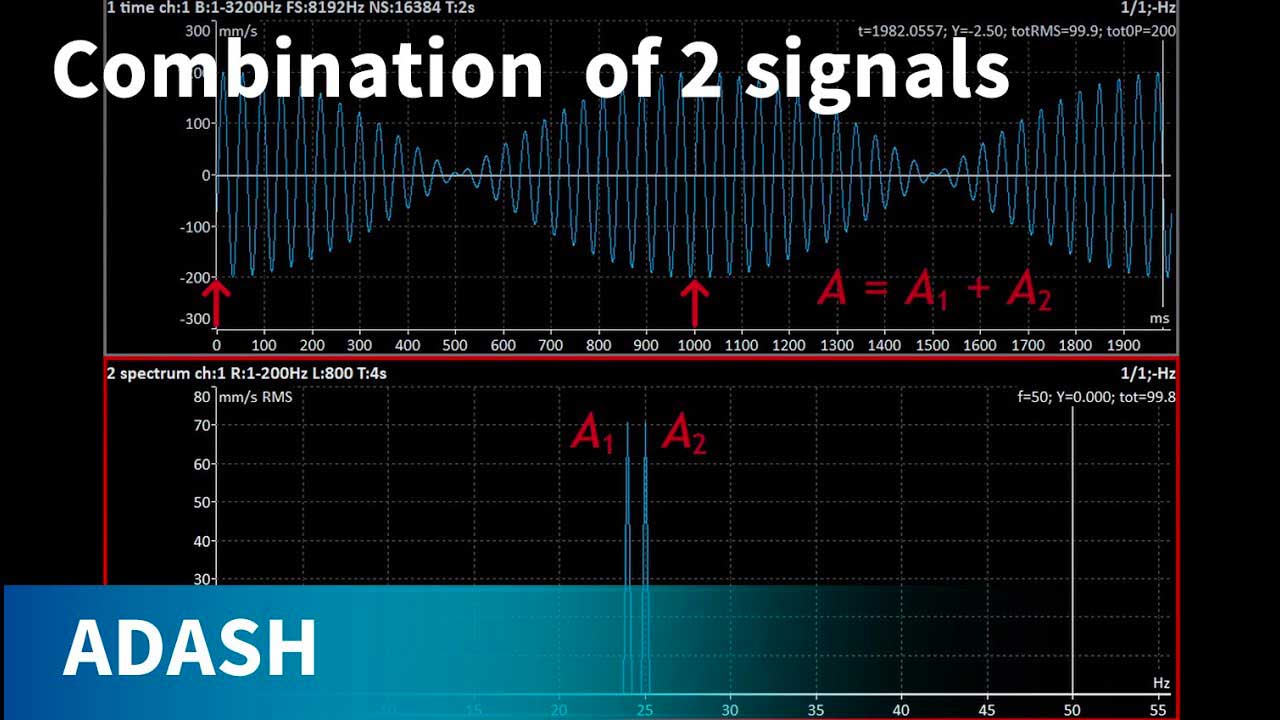
The FFT has one limitation: all signal components must be periodic.
We observe that when the signal is non-periodic, energy "escapes" or "leaks" into several spectral lines close to the actual frequency, causing the spectrum to spread over several lines - this phenomenon is called leakage. To mitigate this, a trick is used: the signal is artificially stitched together using windows, making it periodic.
Vibration analysis can be broadly divided into two categories: machine mechanical fault analysis and bearing analysis. Basic machine mechanical faults include imbalance, misalignment and mechanical looseness. We can detect these faults at low frequencies (10 - 1000 Hz). Vibration measurements are measured in velocity (mm/s). If the velocity values are high, examination of the spectrum can be helpful. If the spectrum shows a single high line at the speed frequency, the fault is imbalance. For example, if there is only one high line at 25 Hz, calculating 25 x 60 gives 1500 RPM. If the speed is indeed 1500 RPM, the fault is imbalance.
Unbalance can be mechanical, requiring balancing, or electrical (in the case of motors). To differentiate, observe the velocity value when the motor is switched off. If the velocity value decreases as the speed decreases, the fault is mechanical unbalance. A rapid drop to almost zero (power cut) indicates an electrical fault. If the speed line and its multiples (harmonics) are present in the spectrum, the fault is looseness or misalignment. Axial velocity values significantly lower than the radial values (e.g. less than 30% of the radial value) suggest looseness. In this case, readings should be taken on all machine feet. This can be done without pads because velocity measurements at low frequencies are less sensitive than high frequency acceleration measurements. Locate the foot with the highest value; it likely points to the looseness failure. This is often due to a broken anchor bolt. If the axial velocity value is similar to or higher than the radial value, the fault is misalignment, which requires alignment. A unique type of fault is resonance, which is mimicked as an unbalance with a single speed line in the spectrum. Balancing will have minimal effect, as the real problem is the natural frequency of the machine foundation near the speed frequency. To identify this, measure the velocity at the foundation. If the values are low at the ends and high in the middle, resonance is the problem. Strengthening of the foundation is usually required - this will change the natural frequency. The other aspect of vibration analysis is bearing analysis. Bearing faults occur in the high frequency range (500 Hz to 16 kHz) and are represented by the bearing vibrations - a tone - caused by ball impacts. Acceleration (g) is used to measure vibration. An increase in vibrations in the high frequency spectrum indicates a worsening bearing condition. Bearing analysis focuses on the fault frequencies that are specific to bearings. What is a bearing fault frequency? Imagine a pitting on the outer race. Each ball hitting the pitting causes a vibration shock (the tone). If there is a crack on the outer race, we calculate the time interval (T) between shocks based on the speed frequency and ball count. This time interval defines the repeating frequency of the shocks - the fault frequency. In this example, it's the fault frequency of the outer race.
But bearing fault frequencies don't appear in the bearing's spectrum; only the vibration frequency from the ball impact (bearing tone) is evident. Such a ball impact can be seen in the time domain:
To identify fault frequencies, signal demodulation is used.