Resonanz - die versteckte Gefahr bei der Wartung von Maschinen
Sie haben Ihre Maschine ordnungsgemäß ausgewuchtet (mindestens zweimal), Sie haben sie ausgerichtet, Sie haben die Befestigungen überprüft und sie vibriert immer noch wie eine alte Waschmaschine, ohne erkennbaren Grund... Der Grund ist wahrscheinlich Resonanz.
MECHANISCHE RESONANZ ist die Tendenz eines mechanischen Systems, mit größerer Amplitude zu reagieren, wenn es mit einer Frequenz vibriert, die seiner Eigenfrequenz entspricht, als wenn es mit anderen Frequenzen vibriert. Jeder mechanische Gegenstand hat Eigenfrequenzen, bei denen er leichter und stärker schwingt als bei anderen Frequenzen.
Sie können dies im täglichen Leben beobachten. Zum Beispiel kann etwas in Ihrem Auto sein, das nicht sehr stark vibriert, aber wenn Sie eine kleine Änderung an der Motordrehzahl vornehmen, werden Sie viel stärkere Vibrationen hören. Dies ist ein Beispiel dafür, dass die Motordrehzahl nahe an der Eigenfrequenz des schwingenden Objekts liegt. Es ist sehr gefährlich, Maschinen in der Nähe ihrer Eigenfrequenz zu betreiben, denn schon eine kleine Unwucht kann extrem hohe Schwingungen erzeugen. Dies kann leicht zur Zerstörung der Maschine führen. Das Resonanzproblem tritt in der Regel am Fundament der Maschine auf. Wenn die Maschinendrehzahl nahe der Eigenfrequenz liegt, messen wir ohne ersichtlichen Grund hohe Schwingungen. Das Wartungsteam führt in der Regel alle Standardverfahren wie Auswuchten, Ausrichten und Überprüfen der Lagermontage durch, aber die Schwingungen bleiben weiterhin hoch.
Das Resonanzproblem ist die Ursache.
Jetzt möchte ich Ihnen erklären, wie Sie die Stoßtestmessung verwenden können. Es ist die perfekte Messung für Situationen, in denen Sie ein Resonanzproblem vermuten. Für diese einfache Demonstration haben wir einen Stahlträger verwendet. Stellen Sie sich vor, es sei ein Maschinenfundament. Wir haben einen Standard-Beschleunigungssensor mit 100 mV/g und einen Hammer verwendet. Die Schwingungsanalysatoren VA4Pro und VA5Pro von Adash verfügen über einen sehr einfach zu bedienenden Stoßtestmodus. Es sind keine Einstellungen erforderlich. Legen Sie den Sensor einfach auf das zu messende Objekt und schlagen Sie mit einem Hammer an. Schauen wir uns die endgültige Grafik an. [1] Die hohen Peaks im Spektrum sind die Eigenfrequenzen, in unserem Fall 100 Hz und 280 Hz. Wenn die Maschinendrehzahl in der Nähe dieser beiden Frequenzen liegt, gibt es ein Resonanzproblem. Wir können die Eigenfrequenz verschieben, um das Problem zu lösen, indem wir die Struktur verstärken, um die Eigenfrequenz zu ändern. Zum Beispiel könnte man in der Mitte eine weitere Stütze einbauen, wodurch die Eigenfrequenzen sinken. [2] In der realen Welt würde ein fester Pfeiler an das Maschinenfundament geschweißt, und die Eigenfrequenzen würden nicht nur verringert, sondern auch neu abgestimmt werden. Jedes mechanische Objekt hat seine Eigenformen.
Ich werde es anhand dieses einfachen freien Balkens erklären (Abbildung 1). Die erste Schwingungsform ist diese: Wir sehen zwei Knoten und drei Gegenknoten. Die nächsten Schwingungsformen haben mehr Knoten und mehr Gegenknoten. Wir werden uns jedoch nur die erste betrachten, deren Eigenfrequenz die niedrigste Eigenfrequenz aus dem gemessenen Diagramm ist. Wir haben mehrere Punkte auf unserem Stahlträger markiert und die Amplitude an jeder Markierung gemessen. Die Länge jedes Pfeils ist proportional zum g-Wert an diesem Punkt. Jetzt sehen Sie die erste Modenform, die wir aus realen Messungen erhalten haben (Abbildung 2).
Bei einfachen Objekten kann man die Modenformen berechnen, aber bei einer komplizierten Konstruktion ist das nicht möglich, man muss sie messen. Wir haben den Rahmen analysiert, indem wir mit einem Hammer ihn angeschlagen haben. Wenn die Maschine in Betrieb ist, kann man auch die Schwingungspegel an jedem Punkt messen. In diesem Fall wird der Rahmen nicht durch den Hammer, sondern durch die Betriebsdrehzahl angeregt. Die Schwingungspegel sind nicht an allen Stellen der Maschine gleich hoch. Wenn man sie alle misst und die Pfeile wieder einzeichnet, erhält man die erste Betriebsablenkungsform der Maschine. Um die nächsten Betriebsablenkungsformen zu finden, müssen Sie das Schwingungsspektrum an jedem Punkt kennen. Die Kenntnis der Maschinenformen ist wichtig für das Verständnis der Maschine.
Die ADASH-Schwingungsanalysatoren verfügen über den ADS-Modus (Animated Deflection Shapes, oder auch Operating deflection shapes). Damit können Sie diese Formen sehr einfach messen und dann die Ergebnisse zur Veranschaulichung animieren. Im nächsten Beispiel werde ich Ihnen zeigen, warum es wichtig ist, die Schwingungsformen zu kennen, die das Schwingungsproblem verursachen. Wir haben den Shaker und das Gummiseil verwendet. Die erste Eigenfrequenz beträgt 10 Hz, und Sie können die erste Modenform sehen (Abbildung 3). Wenn ich den Schwingungspegel reduzieren muss, kann ich die Stütze an vielen Stellen anbringen und es wird funktionieren. Aber manchmal kann die zweite Eigenform das Problem sein und nicht die erste. Jetzt können Sie die zweite Eigenfrequenz sehen (Abbildung 4). Die Position der Stütze ist jetzt viel wichtiger. Wenn ich ihn in die Mitte stelle, bleibt die Schwingung unverändert. Zurück zu unserem ersten Beispiel mit dem Stahlträger. Die ursprüngliche Gesamtschwingung betrug 6,34 g. Wir fügten einen Pfeiler in der Mitte hinzu und die Haupteigenfrequenz bei 100 Hz verringerte sich um das Vierfache. Die zweite Eigenfrequenz bei 280 Hz hat sich jedoch nur um das Zweifache verringert und wirkt sich nun fast genauso stark auf unseren Rahmen aus wie die erste Frequenz. Die Gesamtschwingung beträgt jetzt 3,19 g. Wir haben dann den Pfeiler von der Mitte auf 1/3 der Länge zwischen den Endpfeilern verschoben. Die neuen Eigenfrequenzen lauten wie folgt. [3] Sie sehen, dass die erste Frequenz gleich geblieben ist, aber die zweite hat sich stärker verringert. Die Gesamtschwingung wurde auf 2,56 g reduziert.
DER STOß-TEST IST DIE PERFEKTE MESSUNG FÜR SITUATIONEN, IN DENEN SIE EIN RESONANZPROBLEM VERMUTEN.
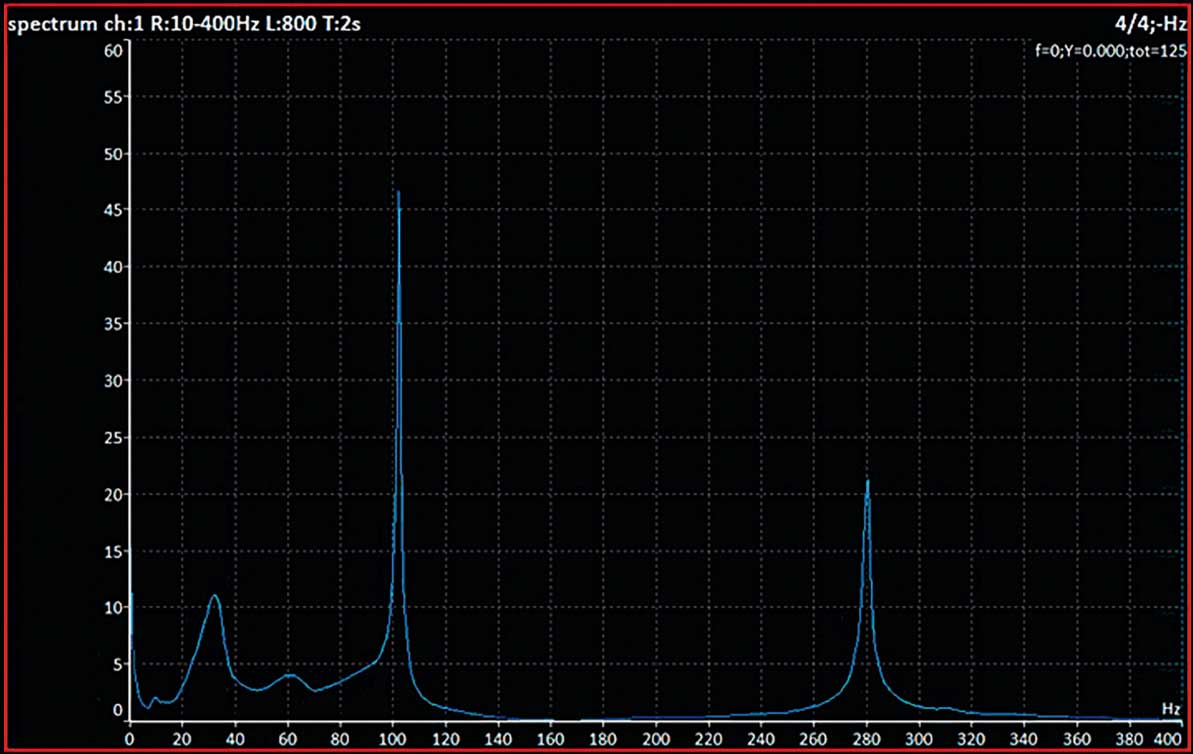
Graph 1: Initial spectrum
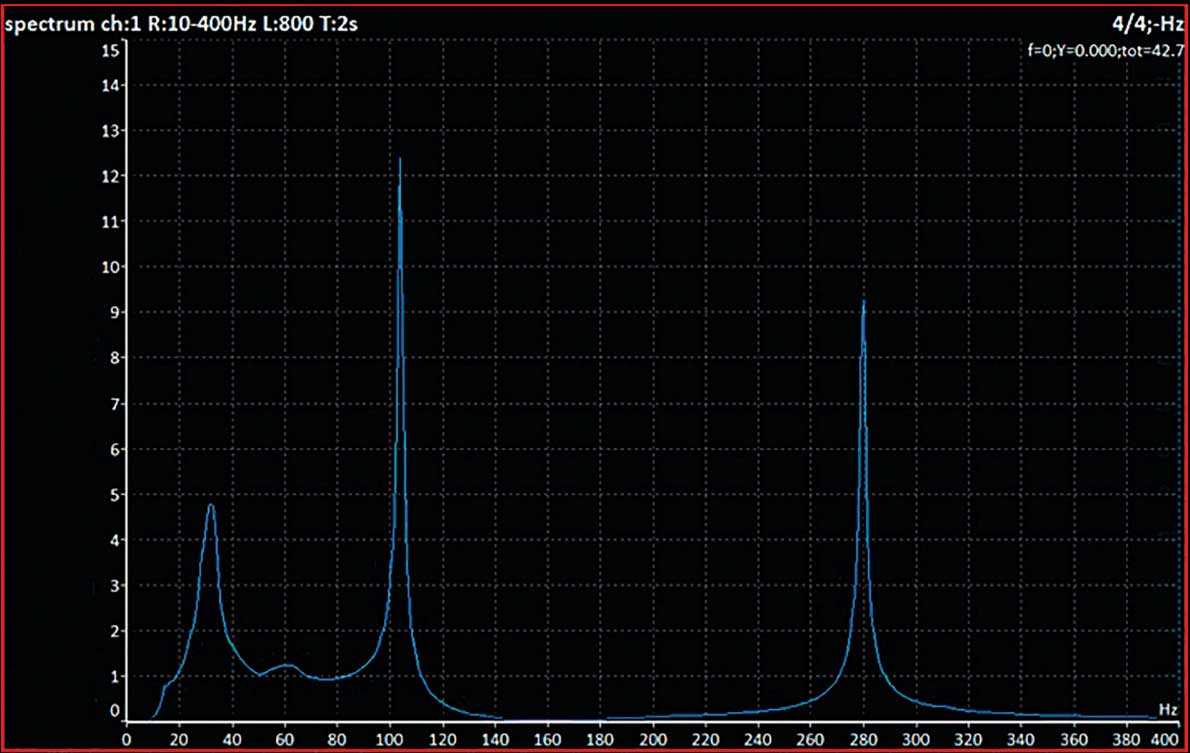
Graph 2: Changed spectrum
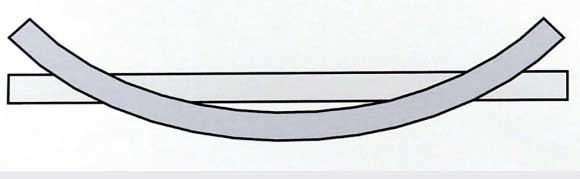
Figure 1: Every mechanical object has its mode shapes.
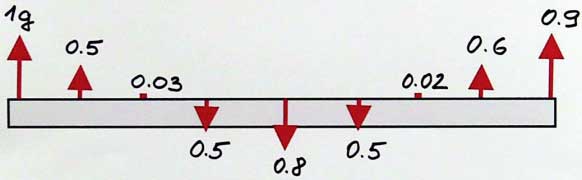
Figure 2: The length of each arrow is proportional to the g value at that point.

Figure 3: The first natural frequency is 10 Hz.

Figure 4: Second natural frequency.
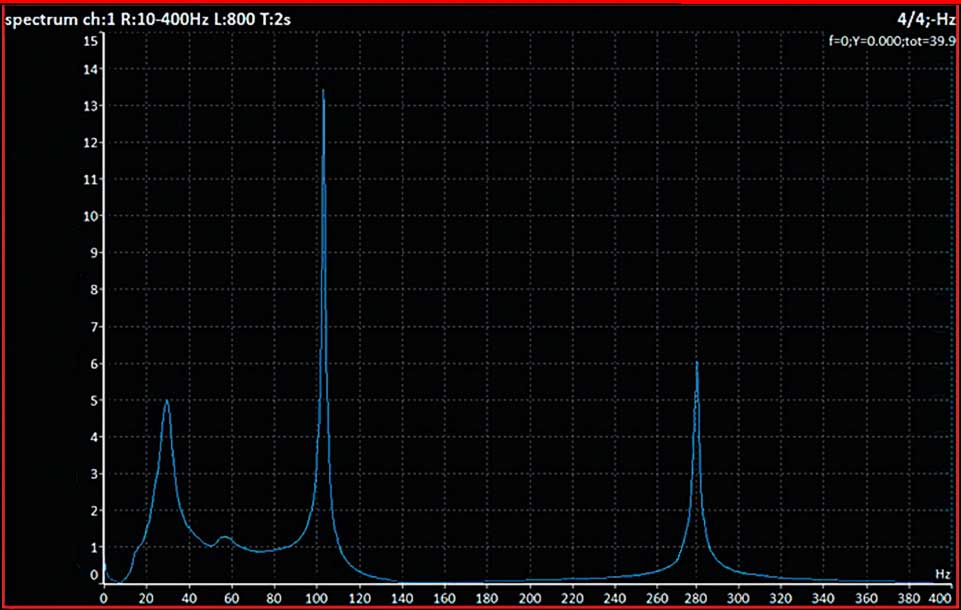
Graph 3: Final spectrum