Die häufigsten Mythen über Beschleunigungssensoren und Frequenzbereich
Der gebräuchlichste Beschleunigungssensor hat eine Empfindlichkeit von 100 mV/g. Der vom Hersteller angegebene Frequenzbereich ist: 0,5 Hz - 15 kHz, mit einer Abweichung von plus oder minus 3 dB. Man könnte meinen, dass +/- 3 dB nicht zu viel ist, dass es sich um etwa +/- 3 Prozent handelt. Aber das ist nicht wahr. Die +/- 3 dB sind viel, viel mehr. Minus 3 dB sind minus 30 Prozent, plus 3 dB sind plus 40 Prozent. Aber der Frequenzbereich ist hier nicht das Hauptthema.
Nehmen wir an, die Antwortfunktion ist flach. Die meisten Nutzer wünschen sich eine sehr niedrige Grenzfrequenz. Sie sagen: "Ich muss eine Maschine mit niedriger Drehzahl messen, meine Maschinendrehzahl beträgt nur 30 U/min, ich muss 0,5 Hz messen". Aber das ist kein relevanter Grund. Ich möchte Ihnen ein Beispiel geben: Wenn ich die Beschleunigung bei einer niedrigen Frequenz messen möchte, welche Beschleunigung kann ich dann erwarten? Wäre es zum Beispiel 1 g? Die meisten Menschen können sich Schwingungsbeschleunigung und Schwingungsgeschwindigkeit nicht vorstellen. Jeder kann sich die Auslenkung vorstellen. Wenn Sie sagen, dass eine Maschine um +/- 3 mm schwingt, dann versteht das jeder. Wir können also diese Formel verwenden, um die Beschleunigung in die Verschiebung und die Verschiebung in die Beschleunigung umzurechnen: acc [m/s2] = Verschiebung [m] * (2 × π × Drehzahl [Hz])2 Mit dieser einfachen Rechnung können wir 1 g in Meter umrechnen. Wenn die Drehzahl 30 U/min beträgt, bedeutet dies 0,5 Hz. (Denken Sie daran, g zuerst in m/s2 umzurechnen.) Die entsprechende Verschiebung ist 1 m. Nicht ein Millimeter, sondern ein Meter. Keine Maschine könnte bei diesem Schwingungsniveau arbeiten. Das entsprechende Schwinggeschwindigkeitsniveau beträgt 3 200 mm/s, das sind 125 ips, unmöglich...
Nehmen wir nun an, dass der Schwingweg 1 mm beträgt. Die entsprechende Beschleunigung beträgt 0,01 m/s2. Das ist 0,001 g. Wenn die Empfindlichkeit des Sensors 100 mV/g beträgt, dann ist die Spannung für 0,001 g - 0,1 mV. Das ist nicht zu viel. Kann man einen solchen Spannungswert messen? Die Antwort lautet NEIN, denn das übliche Sensorrauschen in der Praxis beträgt 0,2 bis 0,4 mV. Bei einem solchen Rauschen ist es sehr schwierig, die 0,1 mV zu messen, da sie unterhalb des Rauschpegels liegen. Aber kehren wir zur Grundfrage zurück. Warum sollte man die Amplitude bei 0,5 Hz messen? Eine andere Antwort lautet: "Ich bräuchte sie, um die Maschine auszuwuchten oder zu prüfen, ob sie schief läuft oder falsch ausgerichtet ist". Ja, in diesen Fällen muss ich den Pegel bei der Drehzahlfrequenz messen, aber das ist nicht notwendig. Wenn die Drehzahl so niedrig ist, sollte man eine Unwucht von mehreren zehn Kilogramm haben, um den Schwingungspegel zu erhöhen. Die Zentrifugalkraft hängt vom Quadrat der Drehzahl ab. Bei 30 Umdrehungen pro Minute wird sie sehr gering sein. Ein weiterer Grund könnte sein, den Zustand des Wälzlagers zu messen.
Und das ist der springende Punkt
Für diese Messung benötige ich die niedrige Frequenz nicht. Wenn die Wälzkörper durch Kratzer, oder wenn Sie so wollen, durch Lagerpittings, auf dem Innen- und Außenring laufen, dann erscheinen die Stöße im Zeitsignal. Die Eigenfrequenzen der Stöße sind sehr hoch. Sie liegen in der Regel zwischen 500 Hz und 25 kHz. Wir brauchen keine niedrigen Frequenzen zu messen, sondern diese sehr hohen Frequenzen. Und das ist bei niedertourigen Wälzlagern (Maschinen) nicht einfach. Wir benötigen eine hohe Auflösung des Signals (hohe Abtastfrequenz) und gleichzeitig ein langes Zeitsignal, da die Zeitspanne zwischen den Stößen sehr lang ist. Die gesamte Messung stellt also hohe Anforderungen an die Datenverarbeitung und die Datenspeicherung. ADASH hat daher die ACMT-Messmethode für die Analyse von Lagern mit niedriger Drehzahl entwickelt und implementiert, die eine intelligente Komprimierung verwendet, um diese Probleme zu überwinden und die meisten Informationen im Schwingungssignal zu erhalten. Das nächste gängige Missverständnis sind die Lagerfehlerfrequenzen. Sie können bei Maschinen mit niedrigen Drehzahlen sehr niedrig sein, und auch hier gehen die Anwender von einer falschen Regel aus. Sie denken vielleicht, dass der Beschleunigungsaufnehmer in der Lage sein muss, diese Frequenzen zu messen. Aber das ist falsch. Die Fehlerfrequenz ist die sich wiederholende Frequenz der Stöße, sie ist keine reine Sinusfrequenz, die von einem Schwingungssensor erfasst werden sollte. Wir müssen die Eigenfrequenzen der Stoßwellen messen. Und die sind wiederum höher als 500 Hz.
DIE EIGENFREQUENZEN VON STÖSSEN SIND SEHR HOCH. SIE LIEGEN TYPISCHERWEISE ZWISCHEN 500 HZ UND 25 KHZ.
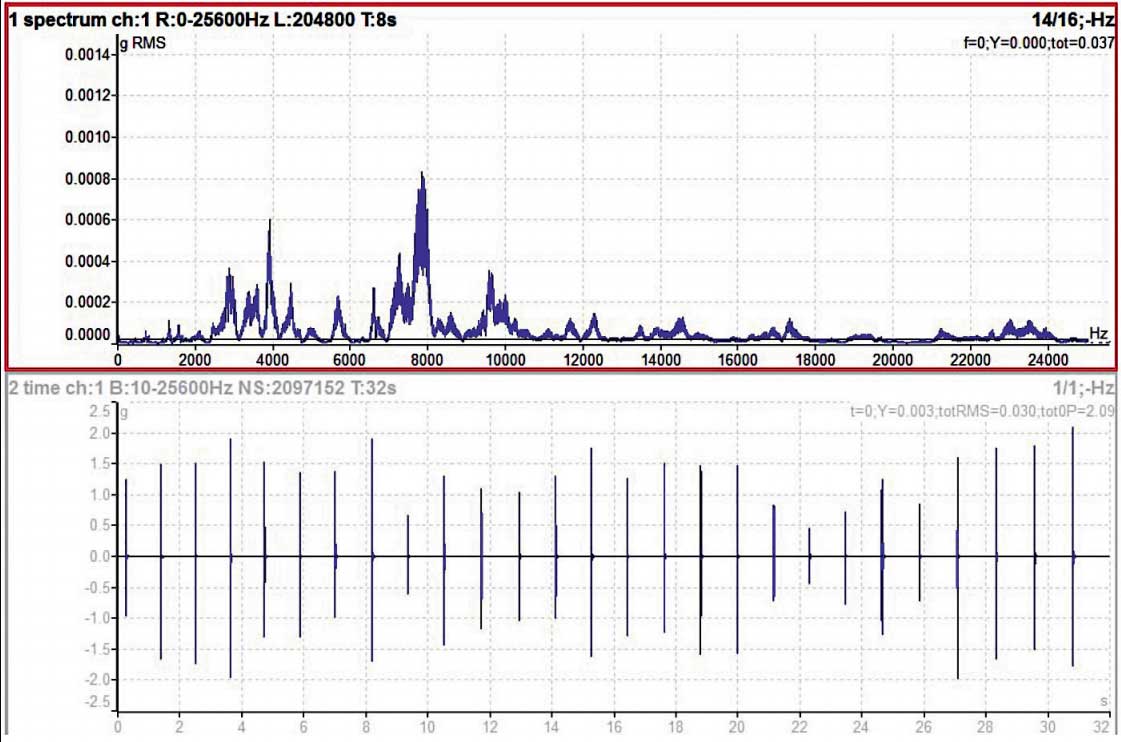
Figure 1
Abbildung 1 zeigt das Schwingungsspektrum und das Zeitsignal (gemessen an einem Wälzlager mit niedriger Drehzahl). Der Bereich liegt bei 25 kHz. Alle Linien mit höherer Amplitude liegen im Bereich von 2 kHz und darüber. Bitte beachten Sie die sehr niedrigen g-Amplituden im Spektrum. Das Spektrum zeigt die Energie des Signals. In diesem Vibrationssignal sehen wir nur Stöße ohne nennenswerte Energie. Aus diesem Grund zeigt das Spektrum sehr niedrige Werte.
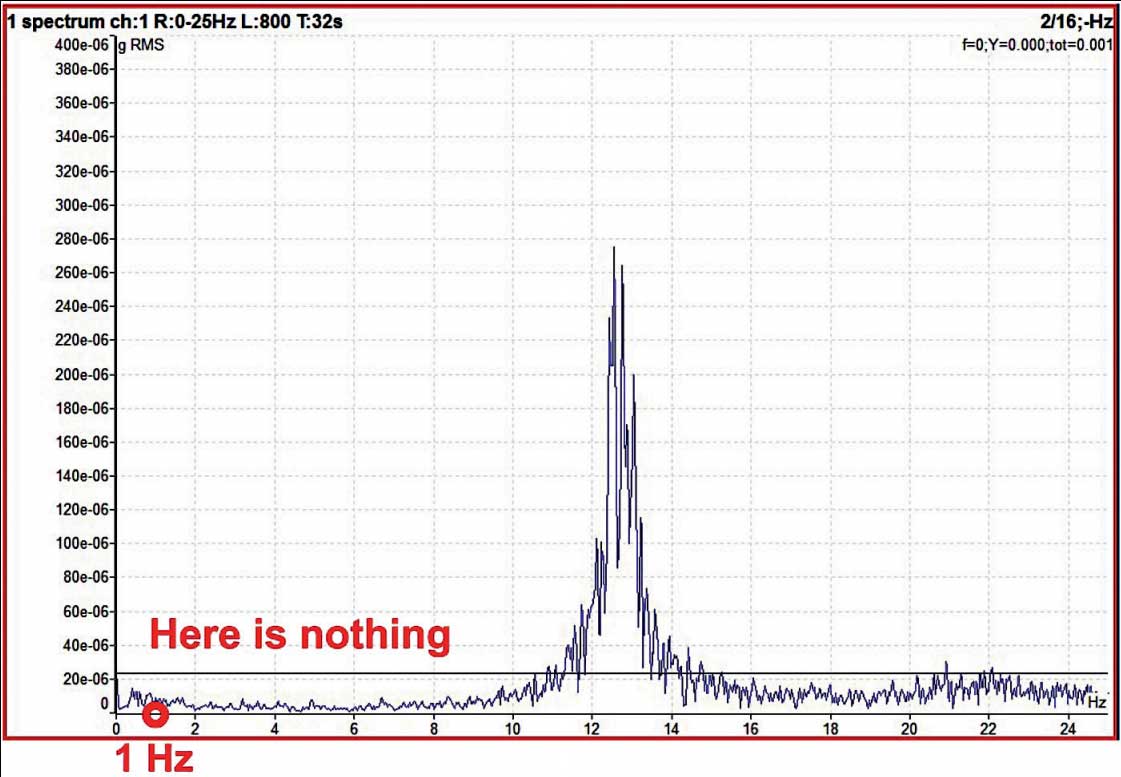
Figure 2
In Abbildung 2 haben wir das Schwingungsspektrum nur im Bereich von 25 Hz gemessen. Die sich wiederholende Frequenz der Stöße für dieses Lager liegt bei 1 Hz. Um 1 Hz herum ist nichts zu sehen. Wenn wir die sich wiederholenden Frequenzen im Spektrum sehen wollen, müssen wir eine Demodulation durchführen. Das heißt, wir müssen die Energie hinzufügen. Das demodulierte Schwingungsspektrum kann etwas Sichtbares zeigen. Das demodulierte Spektrum verwendet das Zeitsignal, das umhüllt wird. Wir wollen nur im Bereich von 500 Hz bis 25 kHz messen. Die niedrigeren Frequenzen interessieren uns nicht. Man kann sich die Einhüllende wie einen einfachen elektrischen Stromkreis vorstellen: Der Impuls kommt und lädt den Kondensator auf, und dann wird der Kondensator durch den Widerstand entladen. Die Entladung ist viel länger als die Dauer des ursprünglichen Impulses. Das ist die zusätzliche Energie, die uns im Spektrum hilft. Und sie hat wirklich geholfen. Im dritten Bild sieht man die 0,85-Hz-Wiederholfrequenz und ihre Oberschwingungen. Die Oberschwingungen treten immer auf, weil das umhüllte Signal verzerrt ist. Es handelt sich nicht um eine reine Sinuswelle, die nur eine Linie im Spektrum zeigen kann.
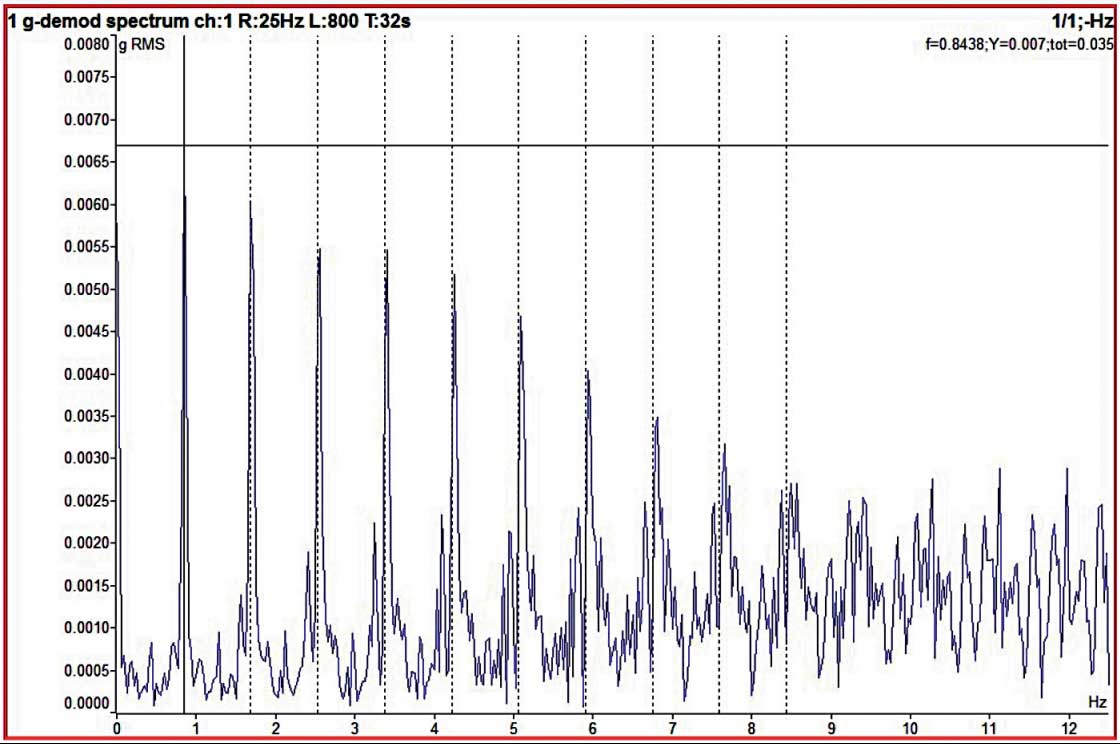
Figure 3